A Compact Ge’ez Characters Alignment on a Standard QWERTY Keyboard Keys
Abstract
This study presents a system and method of Ge’ez character entry on PDAs using a standard QWERTY virtual or PC keyboard. It considers 19 Ge’ez consonant characters and 7 phonetic modifiers as core (default) Ge’ez keyboard keys, and uses only the A-to-Z keys of the standard QWERTY keyboard keys with at most three keystrokes to type every Ge’ez character listed in the Unicode 14.0 Character Code Charts. In this regard, one can type a Ge’ez consonant character by just pressing a keyboard key designated to it, and can modifying it by simply pressing next a Ge’ez phonetic modifier or a hepta-tone of it, if any.
This study adheres to the true nature of Ge’ez scripting and sets forth a number of Ge’ez consonant character groupings of the same sound and/or shape, and key pair alignments that include a number of first keystrokes, and the second keystrokes associated with each first keystroke. Typically, first keystrokes are of Ge’ez consonant character keys, and the second keystrokes are of the Ge’ez phonetic modifier keys. Any other key not paired serves its default function. Keystroke combinations of the conventional keys that include the "Shift" and "Caps-Lock" keys on the QWERTY keyboard are preserved in the present invention as they are used to render Ge’ez consonant characters of same origin but with phonetic and/or shape changes (shifts). All the 563 Ge’ez characters used in modern writing (480 Ge’ez Letter characters, 18 Ge’ez Punctuation characters, 35 Special characters, 20 Ge’ez Numerals, 10 Hindu-Arabic Numerals) are placed on a standard QWERTY keyboard in a compact manner, and in this way, a user can type any Ge’ez character comfortably adhering to its nature and with least finger movements and key recalls.
1. Background
With the advent of personal digital assistants or PDA and digital communications, an efficient digital data encoding method has been a challenge to most phonetic languages [1]. Digital data entry [2] is done with the help of a virtual or a personal computer (PC) keyboard [3] by aligning the keyboard keys to characters used in scripting one's language. A strategic placement of these keys is required with regards to the language's most often characters used and most often characters to follow or precede a certain character in scripting it. Taking into account the number and placement of keys along with the movement of fingers and key recalls one has to make, the efficiency of data entry is, then, determined by the typing speed [4].
Most non-phonetic languages’ characters, with alphabets consisting of consonants and vowels, can be easily mapped on the standard QWERTY keyboard keys with at most two character assignments on a single character key as they have very few characters in their character sets. Such languages can easily have key alignment of their characters with the characters directly mapped and printed on the keyboard keys, called hard mapping. Phonetic languages having characters exceeding the number of keys available on a standard keyboard, however, map multiple characters on a single keyboard key on an attempt to contain all the characters in their character sets. Most keyboard keys are then employed and multiple combinations of keystrokes are applied to access all the mapped characters on a single key. Phonetic languages use soft mapping with the existing standard QWERTY keyboards and attempt to contain and align/map all the characters in their language on the available keys. Strategically mapping all the characters on the available keys of a standard QWERTY keyboard is a challenge most phonetic languages have to consider to improve their efficiency of encodings.
Ge’ez [5], one of the world's most ancient alphabets and languages, is written using a syllabic writing system and is used in East African countries with Semetic origins like in Tigrigna, Amharic, Argoba, Gurage, Harari and etc (Hetrzron, 1997) [6]. Ge’ez is a morphologicaly rich language in which each character of the writing system gets its basic shape from the consonant of the syllable, and the vowel is represented through more or less systematic modifications of these basic shapes (Zitouni, 2014) [7]. It is a phonetic language which embeds phonetics along with the consonant character modifying it accordingly in shape and places only that single but modified character, as opposed to the Latin writing which uses vowels represented as independent character to modify consonant characters and are also laid alongside. Ge’ez is written from left to right across a page. Ge’ez orthography consists of 1st-order characters ("ግዕዝ"/Ge’ez) and character of these 1st-order consonant origins modified by a Ge’ez phonetic modifier [“ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th)], or a “ቤተ፡ሳብእ/Béte-Sabie” sounds of the Ge’ez phonetic modifier [“ቤተ፡ሳብእ ካእብ/Béte-Sabie, Kaeb”(2nd hepta-tone), “ቤተ፡ሳብእ ሳልስ/Béte-Sabie, Salis”(3nd hepta-tone), “ቤተ፡ሳብእ ራብእ/Béte-Sabie, Rabie”(4th hepta-tone), “ቤተ፡ሳብእ ሃሚስ/Béte-Sabie, Hamis”(5th hepta-tone), “ቤተ፡ሳብእ ሳድስ/Béte-Sabie, Sadis”(6th hepta-tone), and “ቤተ፡ሳብእ ሳብእ/Béte-Sabie, Sabie”(7th hepta-tone)]. Thus, "አ" is a 1st-order consonant character, named in the Ge’ez as "አ - ግዕዝ", and the characters "ኡ", "ኢ", "ኣ", "ኤ", "እ", "ኦ", "ⶊ" are derived characters from the consonant character "አ" with the phonetic modifiers [“ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th), and “ቤተ፡ሳብእ ሳብእ/Béte-Sabie, Sabie”(7th hepta-tone)] applied to it respectively, modifying the letter “አ - ካእብ/Kaeb” to “ኡ”, “አ - ሳልስ/Salis” to “ኢ” , “አ - ራብእ/Rabie” to “ኣ”, “አ - ሃሚስ/Hamis” to “ኤ”, “አ - ሳድስ/Sadis” to “እ”, “አ - ሳብእ/Sabie” to “ኦ”, and “አ - ቤተ፡ሳብእ ሳብእ/Béte-Sabie, Sabie” to “ⶊ”. In short, Ge’ez Letters consists of 1st-order consonant characters and characters of these 1st-order consonant origins modified by a Ge’ez phonetic modifier or a hepta-tone of it. In Ge’ez, there is only one spelling (phonetic) for any and every word in the world, with the exception of the Ge’ez alternative representations for some Ge’ez consonant characters like “ጸ" for "ፀ", and "ሠ" for "ሰ”. My first name using Ge’ez Letters is spelled as "ብእምነት", and that is that! However, one may spell it in English (Latin letters) differently: "Bemnet", "Bemnut", "Beimnet", "Bemenet", "Biemnet" etc...
Several schemes have been developed to encode digital Ge’ez data using the standard QWERTY keyboard, and although almost all discrete human sounds can be spelled and with only a single letter in Ge’ez scripting, typing it on a digital media using the existing keyboard alignments, however, is cumbersome to many. This is mainly because these schemes employ most keyboard keys on an attempt to contain all the Ge’ez characters. This makes the most of finger movements to type as they can get scattered all across the keyboard, and makes it hard to recall all the characters and their key positions. In addition, the English (Latin) vowels [a, e, i, o, u] are used to modify a Ge’ez consonant to its phonetic character equivalent, which creates confusion as Latin spellings may differ. Some even use special characters like "]" (or “/”, etc) when run out of Latin vowels to modify Ge’ez consonants. Moreover, one has to press at most 4 to 5 combinations of keystrokes to type a single Ge’ez character.
The dispersed placement of Ge’ez character keys contributes to the movement of fingers and key recalls one has to make. This, along with the confusion of Ge’ez character spelling using English vowels and combination of keys one has to press to type a single Ge’ez character, has made encoding digital Ge’ez contents using the existing schemes undeniably hard, time consuming, and therefore inefficient. It is also contributing its unfair share in letting Ge’ez lose its scripting nature in the digital world. This being the reason, East African countries with Semetic origins, although they have joined the ICT world late, with their ever growing ICT demands and developments, it is believed that not much Geez data has been digitized and made available to the public or the internet.
Adhering to its scripting nature, Ge’ez character entry on PDAs using a standard QWERTY virtual or PC keyboard can be made compact, easy to use, and therefore efficient, by grouping the Ge’ez consonant characters accordingly and employing Ge’ez phonetic modifiers to alter a Ge’ez consonant character to its phonetic equivalent. Therefore, this study aims at designing and developing an efficient Ge’ez character encoding system in PDAs that adheres to the nature of Ge’ez characters scripting for a compact alignment of all the 563 Ge’ez characters (480 Ge’ez Letter characters, 18 Ge’ez Punctuation characters, 35 Special characters, 20 Ge’ez Numerals, 10 Hindu-Arabic Numerals) in the Unicode 14.0 Character Code Charts [8] on a standard QWERTY virtual or PC keyboard that is comfortable and efficient to type with least finger movements and key recalls.
3. Proposed Solution
The generalized model of our proposed solution for the Ge’ez keyboard layout is presented in Figure 3.1. The model is adapted from the work of Aberra Molla - 2017 [17], with the difference in the approach to the keystroke combinations library component. In this component we have used a sensible Ge’ez consonants grouping based on their shape and/or sound, and also have used the nature of Ge’ez scripting to modify a Ge’ez consonant to its phonetic equivalent, which can be considered as a different approach to the task.
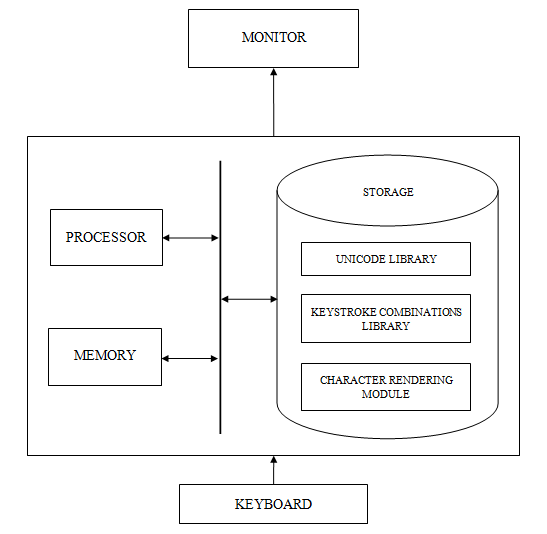 Figure 3.1 General Model of the Proposed Solution
Figure 3.1 General Model of the Proposed Solution
The model consists of a computational device such as a personal digital assistant or PDA, which includes memory for use in connection with the execution of programming instructions by a processor and for the temporary or long-term storage of data and/or program instructions. The computational device may also include data storage for the storage of application programming modules and/or data. The character-rendering, keystroke combinations library and UNICODE library components which do the key alignments of the default keyboard keys to Ge’ez characters may be stored in the data storage. The computational device includes a keyboard input device, which might be virtual (on-screen) or PC (physical) keyboard, and a monitor/display device for output.
The keyboard considered in the proposed solution is a standard QWERTY virtual or PC keyboard. Typing a particular character on a standard QWERTY keyboard includes pressing or striking a particular key, referred to herein as a key-press or a keystroke. A target character is “rendered” on the monitor in response to a key stroke. Rendering, used herein, refers to displaying a character on the monitor, and may additionally include storing or saving the character in a buffer and/or document/file. The standard QWERTY keyboard, in this proposed solution, is used to render Ge’ez characters in the familiar way it is used to render the default keyboard characters. In rendering a Ge’ez character, the target character does not correspond to a character printed on the struck key. The Shift key, used in the conventional way on a standard QWERTY keyboard, is used to map the same key to two different characters, wherein one of the characters is typed using the Shift key. This is the case with the number keys and the symbol keys, which are typed with “default/non-shifted” and “shifted” keystroke combinations, respectively. The shifted characters associated with letter keys, however, correspond to Ge’ez characters with similar shape and/or sound to the default Ge’ez letter keys mapped. Rendering a “shifted” character requires pressing the key while holding down the Shift in a standard QWERTY keyboard. A Ge’ez character is rendered on the monitor based on a mapping between the key that was pressed or struck and the rendered character, which is done by referencing to the keystroke combinations library and the UNICODE library stored in memory or data storage.
The proposed process of rendering a Ge’ez character, which consists of the character-rendering, keystroke combinations library and UNICODE library components is presented in detail in the sections below.
The character-rendering component is responsible for mapping the keystrokes received from the standard QWERTY keyboard to a complete set of Ge’ez characters by referencing to the keystroke combinations library component. In this regard, two or more keystrokes are considered by the character-rendering component to be a “combined keystroke” or “key-pair”. As used herein, a “combined keystroke” or a “key-pair” refers to keystroke combinations that are grouped together for the purpose of typing a particular Ge’ez character. Successive keystrokes are considered independent if they do not have valid associations record in the keystroke combinations library component -- which is responsible for determining the validity of key-pairs. The character-rendering module maps the valid key-pairs to character codes and may consult the UNICODE Library component in retrieving the associated target. The character rendering and key combinations library components can be implemented as discrete elements or as elements of a combined component.
The Keystroke Combinations Library Component contains a list of valid keystroke combinations for all the Ge’ez character sets in the Unicode 14.0 Character Code Charts [8], and is, therefore, responsible for determining the validity of key-pairs received. The systematic grouping of the Ge’ez first-order characters (or “ግእዝ”/Ge’ez) is a prerequisite for an efficient alignment of all the Ge’ez characters on a standard QWERTY keyboard. Therefore, the following grouping is proposed.
Ge’ez first-order consonant characters (“ግእዝ”/Ge’ez) having the same shape and/or sound origins but with the relatively most changes (shifts) in shape and/or sound are grouped in to two major groups using the Shift key function. Each “shifted” or “non-shifted/default” Ge’ez first-order consonant characters may also have an alternative representation of it or a hepta-tonic representation called “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” and a 2nd hepta-tonic representation called “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” Ge’ez first-order consonant character of it. Each Ge’ez first-order consonant may then have associated letter representations of it altered by the Ge’ez phonetic modifiers [“ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th)], or a “ቤተ፡ሳብእ/Béte-Sabie” (hepta-tone) of them [“ቤተ፡ሳብእ ካእብ/Béte-Sabie, Kaeb”(2nd hepta-tone), “ቤተ፡ሳብእ ሳልስ/Béte-Sabie, Salis”(3nd hepta-tone), “ቤተ፡ሳብእ ራብዕ/Béte-Sabie, Rabie”(4th hepta-tone), “ቤተ፡ሳብእ ሃሚስ/Béte-Sabie, Hamis”(5th hepta-tone), “ቤተ፡ሳብእ ሳድስ/Béte-Sabie, Sadis”(6th hepta-tone), and “ቤተ፡ሳብእ ሳብዕ/Béte-Sabie, Sabie”(7th hepta-tone)], if any, implemented by pressing along with the Shift key.
19 Ge’ez first-order (“ግእዝ”/Ge’ez) consonant letter characters and 7 Ge’ez phonetic modifiers are identified as core (default) Ge’ez keys in this study. These 19 Ge’ez first-order consonants are considered as the most frequently used Ge’ez first-order consonants in Ge’ez scripting. The rest Ge’ez first-order (“ግእዝ”/Ge’ez) consonant letter characters are grouped according to their similarity in sound and/or shape to the 19 core Ge’ez first-order (“ግእዝ”/Ge’ez) consonant letter characters identified. For example, the “ከ, ኰ, ⷈ ,ኸ, ዀ, ⷐ” Ge’ez first-order (“ግእዝ”/Ge’ez) consonant letter characters are grouped together to a single keyboard key, with the “ከ, ኰ, ⷈ” belonging to “ከ” which can be accessed through a designated keyboard key on default, and the “ኸ, ዀ, ⷐ” belonging to “ኸ” which can be accessed through the designated keyboard key to the “ከ” along with the Shift key. Nested groups of the “ከ” key which are “ኰ” and “ⷈ” can be accessed by keystroke combination of the designated key for “ከ” along with the “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” hepta-tonic and the “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” 2nd hepta-tonic Ge’ez modifiers, respectively. The same goes for the nested groups of the “ኸ” key which are “ዀ” and “ⷐ”. This way a single keybaord key be aligned to a maximum of 6 Ge’ez first-order (“ግእዝ”/Ge’ez) consonant letter characters, and the grouping is transparent to understand and recall.
The grouping of the core 19 Ge’ez first-order consonants identified and their alignment on the A-Z keys of the standard QWERTY keyboard is presented in Table 3.1.
| # | Key | Default | Default, then b | Default + Shift, then b | Default + Shift | Default + Shift, then b | Default + Shift, then Shift + b |
|---|---|---|---|---|---|---|---|
| 1 | q | ቀ | ቈ | ⷀ | ቐ | ቘ | |
| 2 | w | መ | ᎀ | ወ | |||
| 3 | e | ሰ | ሠ | ꬁ | ሸ | ⶠ | |
| 4 | r | ረ | |||||
| 5 | t | ተ | ቸ | ⶨ | |||
| 6 | y | የ | |||||
| 7 | u | ገ | ጐ | ⷘ | ጘ | ⶓ | |
| 8 | i | ከ | ኰ | ⷈ | ኸ | ዀ | ⷐ |
| 9 | o | ሀ | ኀ | ኈ | ሐ | 𞟨 | 𞟠 |
| 10 | p | ደ | ዸ | ꬉ | ጀ | ||
| 11 | a | አ | ኧ | ዐ | |||
| 12 | s | “ካእብ” | “ቤተ፡ሳብእ ካእብ” | ||||
| 13 | d | “ሳልስ” | “ቤተ፡ሳብእ ሳልስ” | ||||
| 14 | f | “ራብእ” | “ቤተ፡ሳብእ ሳልስ” | ||||
| 15 | g | በ | ᎄ | ቨ | |||
| 16 | h | ለ | |||||
| 17 | j | “ሃሚስ” | “ቤተ፡ሳብእ ሃሚስ” | ||||
| 18 | k | “ሳድስ” | “ቤተ፡ሳብእ ሳድስ” | ||||
| 19 | l | “ሳብእ” | “ቤተ፡ሳብእ ሳብእ” | ||||
| 20 | z | ዘ | ꬑ | ዠ | ⶰ | ||
| 21 | x | ፀ | ጸ | ꬨ | ጰ | ||
| 22 | c | ፈ | ᎈ | ||||
| 23 | v | ጠ | ጨ | ⶸ | ꬠ | ||
| 24 | b | “ቤተ፡ሳብእ ግእዝ” | “ክሌቱ, ቤተ፡ሳብእ ግእዝ” | ||||
| 25 | n | ነ | ኘ | ||||
| 26 | m | ፐ | ᎌ |
The general guidelines for the valid keystroke combinations in this work are based on the following rules.
- Pressing a designated default/core Ge’ez character key yields the associated “default” Ge’ez core character, shown in Table 3.1 and Figure 3.2.
- Pressing a designated default/core Ge’ez character key along with the Shift key yields the associated “shifted” Ge’ez core characters, shown in Table 3.1 and Figure 3.3.
- The Shift key along with the Ge’ez modifier sets the phonetic modifiers to the next hepta-tonic level phonetic modifier.
- A modifier key is considered only if the character rendered before it is of Ge’ez first-order (“ግእዝ”/Ge’ez) character (first-order Letter, Number, or Punctuation) type, and there must be a related character associated with the first-order Ge’ez character rendered and the Ge’ez phonetic modifier key pressed in the Keystroke Combinations Library.
- Pressing the “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key after a Ge’ez first-order (“ግእዝ”/Ge’ez) character rendered retrieves an alternative representation of it, if any, or a “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) Ge’ez character representation of it, if any.
- If the “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key is pressed along with the Shift key, it turns in to a “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic) modifier and yields a “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic) Ge’ez character representation of a Ge’ez first-order character (“ግእዝ”/Ge’ez) rendered before it.
- Every Ge’ez first-order character (“ግእዝ”/Ge’ez) rendered may have associated characters that can be accessed with a keystroke of the Ge’ez phonetic modifier keys [“ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th)], or a “ቤተ፡ሳብእ/Béte-Sabie” (hepta-tonic) of them when pressed along with the shift key [“ቤተ፡ሳብእ ካእብ/Béte-Sabie, Kaeb”(2nd hepta-tone), “ቤተ፡ሳብእ ሳልስ/Béte-Sabie, Salis”(3nd hepta-tone), “ቤተ፡ሳብእ ራብዕ/Béte-Sabie, Rabie”(4th hepta-tone), “ቤተ፡ሳብእ ሃሚስ/Béte-Sabie, Hamis”(5th hepta-tone), “ቤተ፡ሳብእ ሳድስ/Béte-Sabie, Sadis”(6th hepta-tone), and “ቤተ፡ሳብእ ሳብዕ/Béte-Sabie, Sabie”(7th hepta-tone)], if any.
 Figure 3.2 Ge’ez first-order Characters On Default
Figure 3.2 Ge’ez first-order Characters On Default
 Figure 3.3 Shifted Ge’ez first-order Characters
Figure 3.3 Shifted Ge’ez first-order Characters
This study considers the Ge’ez phonetic modifier keys as the most often pressed keys in Ge’ez scripting. These keys, therefore, require strategic placement to minimize finger movements. The (A), (S), (D), (F), and (J), (K), (L), (;) keys are the default positions of the left and right hand fingers on a standard QWERTY keyboard, respectively. We have, therefore, mapped the Ge’ez phonetic modifier keys to the default finger positions on a standard QWERTY keyboard starting from the (S)-to(L) keys as “ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th)], respectively. The (A) key is mapped to the (አ) Ge’ez first-order consonant key for easiness in associating the phonetic variations of the (አ) Ge’ez first-order consonant to [ኡ, ኢ, ኣ, ኤ, እ, ኦ], and thus to easily understanding the phonetic modifier keys' formations, i.e., in a row as in “ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th)], respectively.
The “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key assumes the position of the (B) letter key on a standard QWERTY keyboard. This modifier key is placed strategically in the middle, (B) key, right below the default finger positions to be accessed by both left and right hand fingers while at the same time distributing its key-press loads (for load balancing). This modifier key is the only modifier key that can be applied to all the Ge’ez first-order characters (Letters, Numbers, and Punctuations), serving slightly different functions in all. The “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key, when pressed after a Ge’ez first-order consonant rendered, is used to modify it to yield its alternative representation, first, or a “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) associated Ge’ez first-order consonant, second, if any, on default. When pressed along with the Shift key, it is used to render a related but of a “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic) first-order consonant of the Ge’ez first-order consonant typed before it, if any.
The 19 core Ge’ez first-order consonants identified and the 7 Ge’ez phonetic modifier are aligned to only the 26 A-Z letter keys of a standard QWERTY keyboard (see Table 3.1) making the key alignment compact for smooth and least finger movements. The default/core 19 Ge’ez first-order consonant keys mapped can also retrieve another 14 Ge’ez first-order consonants when pressed along with the Shift key. Each core Ge’ez first-order consonant keys on default may have another associated “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) or “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic) Ge’ez first-order consonants. Each shifted Ge’ez first-order consonant keys may also have associated “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) or “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic)Ge’ez first-order consonants. A total of 64 Ge’ez first-order consonant are considered in this study, and their associeted phonetic characters are presented in Table 3.2.
There are 480 Ge’ez letter characters listed in the Table 3.2 that can be rendered by modifying the 64 Ge’ez first-order consonants with the phonetic modifier keys [“ካእብ/Kaeb”(2nd), “ሳልስ/Salis”(3rd), “ራብእ/Rabie”(4th), “ሃሚስ/Hamis”(5th), “ሳድስ/Sadis”(6th), “ሳብእ/Sabie”(7th)], or a “ቤተ፡ሳብእ/Béte-Sabie” (hepta-tonic) of them when pressed along with the Shift key [“ቤተ፡ሳብእ ካእብ/Béte-Sabie, Kaeb”(2nd hepta-tone), “ቤተ፡ሳብእ ሳልስ/Béte-Sabie, Salis”(3nd hepta-tone), “ቤተ፡ሳብእ ራብዕ/Béte-Sabie, Rabie”(4th hepta-tone), “ቤተ፡ሳብእ ሃሚስ/Béte-Sabie, Hamis”(5th hepta-tone), “ቤተ፡ሳብእ ሳድስ/Béte-Sabie, Sadis”(6th hepta-tone), and “ቤተ፡ሳብእ ሳብዕ/Béte-Sabie, Sabie”(7th hepta-tone)], if any.
| # | First order Ge’ez (“ግእዝ” / Ge’ez) | ካእብ / Kaeb (s) | ሳልስ / Salis (d) | ራብእ / Rabie (f) | ሃሚስ / Hamis (j) | ሳድስ / Sadis (k) | ሳብእ / Sabie (l) | ቤተ፡ሳብእ - ግእዝ / Béte-Sabie, Ge’ez (b) | ቤተ፡ሳብእ ካእብ / Béte-Sabie Kaeb (S) | ቤተ፡ሳብእ ሳልስ / Béte-Sabie Salis (D) | ቤተ፡ሳብእ ራብእ / Béte-Sabie Rabie (F) | ቤተ፡ሳብእ ሃሚስ / Béte-Sabie Hamis (J) | ቤተ፡ሳብእ ሳድስ / Béte-Sabie Sadis (K) | ቤተ፡ሳብእ ሳብእ / Béte-Sabie Sabie (L) | ክሌቱ ቤተ፡ሳብእ - ግእዝ / Klétu Béte-Sabie, Ge’ez (B) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ቀ | ቁ | ቂ | ቃ | ቄ | ቅ | ቆ | ቈ | ቊ | ቋ | ቌ | ቍ | ቇ | ||
| 2 | ቈ | 𞟰 | 𞟱 | 𞟲 | |||||||||||
| 3 | ⷀ | ⷁ | ⷂ | ⷃ | ⷄ | ⷅ | ⷆ | ||||||||
| 4 | ቐ | ቑ | ቒ | ቓ | ቔ | ቕ | ቖ | ቘ | ቚ | ቛ | ቜ | ቝ | |||
| 5 | ቘ | ||||||||||||||
| 6 | መ | ሙ | ሚ | ማ | ሜ | ም | ሞ | ᎀ | ᎁ | ሟ | ᎂ | ⶁ | |||
| 7 | ᎀ | 𞟭 | 𞟮 | ᎃ | ፙ | ||||||||||
| 8 | ወ | ዉ | ዊ | ዋ | ዌ | ው | ዎ | ||||||||
| 9 | ሰ | ሱ | ሲ | ሳ | ሴ | ስ | ሶ | ሠ | ሷ | ⶃ | ꬁ | ||||
| 10 | ꬁ | ꬂ | ꬃ | ꬄ | ꬅ | ꬆ | |||||||||
| 11 | ሠ | ሡ | ሢ | ሣ | ሤ | ሥ | ሦ | ሧ | |||||||
| 12 | ሸ | ሹ | ሺ | ሻ | ሼ | ሽ | ሾ | ⶠ | ሿ | ⶄ | |||||
| 13 | ⶠ | ⶡ | ⶢ | ⶣ | ⶤ | ⶥ | ⶦ | ||||||||
| 14 | ረ | ሩ | ሪ | ራ | ሬ | ር | ሮ | ፘ | ሯ | ⶂ | |||||
| 15 | ተ | ቱ | ቲ | ታ | ቴ | ት | ቶ | ቷ | ⶆ | ||||||
| 16 | ቸ | ቹ | ቺ | ቻ | ቼ | ች | ቾ | ⶨ | ቿ | ⶇ | |||||
| 17 | ⶨ | ⶩ | ⶪ | ⶫ | ⶬ | ⶭ | ⶮ | ||||||||
| 18 | የ | ዩ | ዪ | ያ | ዬ | ይ | ዮ | ዯ | |||||||
| 19 | ገ | ጉ | ጊ | ጋ | ጌ | ግ | ጎ | ጐ | ጒ | ጓ | ጔ | ጕ | ጏ | ⷘ | |
| 20 | ጐ | 𞟸 | 𞟹 | 𞟺 | |||||||||||
| 21 | ⷘ | ⷙ | ⷚ | ⷛ | ⷜ | ⷝ | ⷞ | ||||||||
| 22 | ጘ | ጙ | ጚ | ጛ | ጜ | ጝ | ጞ | ⶓ | ⶔ | ጟ | ⶕ | ⶖ | |||
| 23 | ⶓ | ||||||||||||||
| 24 | ከ | ኩ | ኪ | ካ | ኬ | ክ | ኮ | ኰ | ኲ | ኳ | ኴ | ኵ | ኯ | ⷈ | |
| 25 | ኰ | 𞟵 | 𞟶 | 𞟷 | |||||||||||
| 26 | ⷈ | ⷉ | ⷊ | ⷋ | ⷌ | ⷍ | ⷎ | ||||||||
| 27 | ኸ | ኹ | ኺ | ኻ | ኼ | ኽ | ኾ | ዀ | ዂ | ዃ | ዄ | ዅ | ⷐ | ||
| 28 | ዀ | ||||||||||||||
| 29 | ⷐ | ⷑ | ⷒ | ⷓ | ⷔ | ⷕ | ⷖ | ||||||||
| 30 | ሀ | ሁ | ሂ | ሃ | ሄ | ህ | ሆ | ኀ | ሇ | ኈ | |||||
| 31 | ኀ | ኁ | ኂ | ኃ | ኄ | ኅ | ኆ | ኊ | ኋ | ኌ | ኍ | ኇ | |||
| 32 | ኈ | ||||||||||||||
| 33 | ሐ | ሑ | ሒ | ሓ | ሔ | ሕ | ሖ | 𞟨 | ሗ | 𞟠 | |||||
| 34 | 𞟨 | 𞟩 | 𞟪 | 𞟫 | |||||||||||
| 35 | 𞟠 | 𞟡 | 𞟢 | 𞟣 | 𞟤 | 𞟥 | 𞟦 | ||||||||
| 36 | ደ | ዱ | ዲ | ዳ | ዴ | ድ | ዶ | ዸ | ዷ | ⶌ | ꬉ | ||||
| 37 | ዸ | ዹ | ዺ | ዻ | ዼ | ዽ | ዾ | ዿ | ⶍ | ||||||
| 38 | ꬉ | ꬊ | ꬋ | ꬌ | ꬍ | ꬎ | |||||||||
| 39 | ጀ | ጁ | ጂ | ጃ | ጄ | ጅ | ጆ | ጇ | ⶎ | ||||||
| 40 | አ | ኡ | ኢ | ኣ | ኤ | እ | ኦ | ኧ | ⶊ | ||||||
| 41 | ኧ | ||||||||||||||
| 42 | ዐ | ዑ | ዒ | ዓ | ዔ | ዕ | ዖ | ||||||||
| 43 | በ | ቡ | ቢ | ባ | ቤ | ብ | ቦ | ᎄ | ᎅ | ቧ | ᎆ | ⶅ | |||
| 44 | ᎄ | 𞟳 | 𞟴 | ᎇ | |||||||||||
| 45 | ቨ | ቩ | ቪ | ቫ | ቬ | ቭ | ቮ | ቯ | |||||||
| 46 | ለ | ሉ | ሊ | ላ | ሌ | ል | ሎ | ሏ | ⶀ | ||||||
| 47 | ዘ | ዙ | ዚ | ዛ | ዜ | ዝ | ዞ | ꬑ | ዟ | ⶋ | |||||
| 48 | ꬑ | ꬒ | ꬓ | ꬔ | ꬕ | ꬖ | |||||||||
| 49 | ዠ | ዡ | ዢ | ዣ | ዤ | ዥ | ዦ | ⶰ | ዧ | ||||||
| 50 | ⶰ | ⶱ | ⶲ | ⶳ | ⶴ | ⶵ | ⶶ | ||||||||
| 51 | ፀ | ፁ | ፂ | ፃ | ፄ | ፅ | ፆ | ጸ | ፇ | ꬨ | |||||
| 52 | ጸ | ጹ | ጺ | ጻ | ጼ | ጽ | ጾ | ጿ | |||||||
| 53 | ꬨ | ꬩ | ꬪ | ꬫ | ꬬ | ꬭ | ꬮ | ||||||||
| 54 | ጰ | ጱ | ጲ | ጳ | ጴ | ጵ | ጶ | ጷ | ⶑ | ||||||
| 55 | ፈ | ፉ | ፊ | ፋ | ፌ | ፍ | ፎ | ᎈ | ᎉ | ፏ | ᎊ | ᎋ | |||
| 56 | ᎈ | 𞟻 | 𞟼 | ፚ | |||||||||||
| 57 | ጠ | ጡ | ጢ | ጣ | ጤ | ጥ | ጦ | ጧ | ⶏ | ||||||
| 58 | ጨ | ጩ | ጪ | ጫ | ጬ | ጭ | ጮ | ⶸ | ጯ | ⶐ | ꬠ | ||||
| 59 | ⶸ | ⶹ | ⶺ | ⶻ | ⶼ | ⶽ | ⶾ | ||||||||
| 60 | ꬠ | ꬡ | ꬢ | ꬣ | ꬤ | ꬥ | ꬦ | ||||||||
| 61 | ነ | ኑ | ኒ | ና | ኔ | ን | ኖ | ኗ | ⶈ | ||||||
| 62 | ኘ | ኙ | ኚ | ኛ | ኜ | ኝ | ኞ | ኟ | ⶉ | ||||||
| 63 | ፐ | ፑ | ፒ | ፓ | ፔ | ፕ | ፖ | ᎌ | ᎍ | ፗ | ᎎ | ⶒ | |||
| 64 | ᎌ | 𞟽 | 𞟾 | ᎏ |
Table 3.3 presents the key alignments of the standard QWERTY keyboard punctuation and symbol characters to the associated Ge’ez first-order (most frequently used) punctuation and special characters in Ge’ez scripting. All the punctuation and special characters on a default QWERTY keyboard, and all the Ge’ez punctuation and symbol characters in the UNICODE version 14.0 character sets are considered in this study. Related Ge’ez punctuation and symbol characters are grouped together based on the function and/or shape of characters for an easy character key recall. Grouped characters are, then, mapped on a single key retrieving different characters on default and when “shifted”. The “non-shifted/default“ or “shifted” Ge’ez first-order (most frequently used) characters mapped can also be modified to access related characters of same origin, if any, by pressing next the “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key without the Shift key, or “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic) along with the Shift key.
| # | QWERTY Character | Mapped Character on Default | Default, then “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” | Default, then Shift + “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” |
|---|---|---|---|---|
| 1 | ` | ` | ||
| 2 | ~ | ~ | ᎕ | |
| 3 | ! | ! | ¡ | |
| 4 | @ | @ | ||
| 5 | # | # | ||
| 6 | $ | $ | ||
| 7 | % | % | ||
| 8 | ^ | ^ | ᎔ | ᎑ |
| 9 | & | & | ||
| 10 | * | * | ፠ | ፨ |
| 11 | ( | ( | ||
| 12 | ) | ) | ||
| 13 | - | - | ||
| 14 | _ | _ | ᎗ | ᎘ |
| 15 | = | = | ||
| 16 | + | + | ||
| 17 | [ | [ | ||
| 18 | ] | ] | ||
| 19 | { | { | ||
| 20 | } | } | ||
| 21 | \ | \ | ||
| 22 | | | | | ᎙ | |
| 23 | ; | ፡ | ። | ; |
| 24 | : | ፥ | ፤ | ፦ |
| 25 | ' | ' | ፟ | |
| 26 | " | " | ||
| 27 | , | ፣ | ᎖ | , |
| 28 | < | < | « | |
| 29 | . | . | ᎐ | : |
| 30 | > | > | » | |
| 31 | / | / | ||
| 32 | ? | ? | ፧ |
The key alignment of the Arabic Number keys to their equivalent single-digit Ge’ez first-order (single-digit) Numerals is presented in Table 3.4. The alignment is based on the equivalent representation of the single digit Arabic numerals with Ge’ez numerals, except for the Arabic numeral "0". When the “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key is pressed after a Ge’ez first-order (single-digit) Number typed, it retrieves a tenth (10th) digit representation of the single-digit Ge’ez first-order numbers, if any, on default. Pressing the “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” (hepta-tonic) modifier key along with the shift-key turns it to a “ክሌቱ ቤተ፡ሳብእ - ግእዝ/Klétu Béte-Sabie, Ge’ez” (2nd hepta-tonic) modifier, and renders the associated Arabic single digit numbers.
| # | QWERTY Character | Mapped Character on Default | Default, then “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” | Default, then Shift + “ቤተ፡ሳብእ ግእዝ/Béte-Sabie, Ge’ez” |
|---|---|---|---|---|
| 1 | 0 | 0 | ፻ | ፼ |
| 2 | 1 | ፩ | ፲ | 1 |
| 3 | 2 | ፪ | ፳ | 2 |
| 4 | 3 | ፫ | ፴ | 3 |
| 5 | 4 | ፬ | ፵ | 4 |
| 6 | 5 | ፭ | ፶ | 5 |
| 7 | 6 | ፮ | ፷ | 6 |
| 8 | 7 | ፯ | ፸ | 7 |
| 9 | 8 | ፰ | ፹ | 8 |
| 10 | 9 | ፱ | ፺ | 9 |
The flowchart in Figure 3.3 summarizes the proposed process of Ge’ez character entry in this study. A keystroke received is first checked to determine if it is designated to a character. If the received keystroke is a character key, it is then examined to see if it is a designated Ge’ez key. If the character key is not a designated Ge’ez key, the default character is rendered. If the character key is a designated Ge’ez key, it is then examined again to check if it is of a Ge’ez phonetic modifier type. If it is not a Ge’ez phonetic modifier, the designated Ge’ez character is rendered. However, if the keystroke received is of a Ge’ez phonetic modifier type, the last character rendered is checked to see if it is of a Ge’ez first-order character type. If the last character rendered is of a Ge’ez first-order character type and has a related character associated with the Ge’ez phonetic modifier keystroke received, it is removed and replaced by the related and modified Ge’ez character. Any other keyboard keystroke received serves its default function/s.
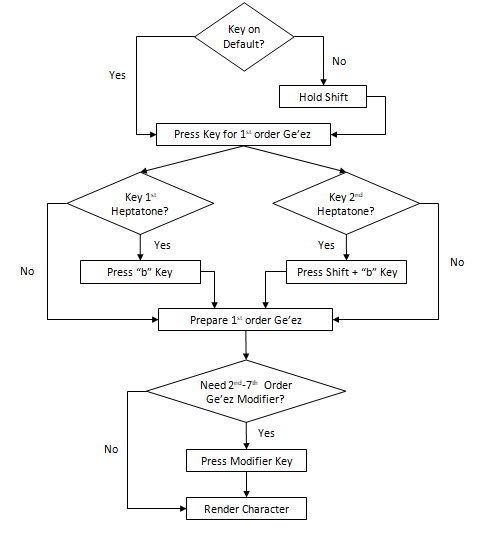 Figure 3.4 flowchart for the Proposed Ge’ez Character Entry
Figure 3.4 flowchart for the Proposed Ge’ez Character Entry
4. Conclusion and Future Work
Conclusion
In this work, we have grouped Ge’ez first-order characters (ግእዝ) by shape and/or sound resemblance and aligned grouped characters on a single key of the QWERTY keyboard keys. We have used Ge’ez character shape and/or sound modifiers to modifiy a Ge’ez first-order character (ግእዝ) to its phonetic equivalent. 19 Ge’ez first-order characters (ግእዝ) were identified, by their frequency in Ge’ez scripting, as core/default Ge’ez characters into which the rest Ge’ez first-order characters were grouped in. 7 Ge’ez shape and/or sound modifiers were also used. The 19 core/default Ge’ez first-order characters (ግእዝ) and the 7 Ge’ez shape and/or sound modifiers were aligned on the A-to-Z letter characters of the standard QWERTY keyboard, making the alignment compact for smooth finger movement and key recall in typing.
Ge’ez soft keyboard layout can be made compact with high key-recalls - and thus, efficient in typing - by adhering to the Ge’ez scipting nature.
Contribution
The main contributions of the study are listed below.
- A new, compact and efficient soft Ge’ez keyboard layout is presented.
- The grouping of the Ge’ez first-order characters (ግእዝ) by shape and/or sound resemblance.
- The modification of Ge’ez first-order (ግእዝ) characters into their phonetic equivalent using Ge’ez character shape and/or sound modifiers, or their heptatonics (“ቤተ፡ሳብእ”).
- The modification of Ge’ez first-order characters (ግእዝ) characters into their shape and/or sound varieties using Ge’ez heptatonic (“ቤተ፡ሳብእ ግእዝ”) or 2nd heptatonic (“ክሌቱ, ቤተ፡ሳብእ ግእዝ”) first-order (ግእዝ) shape and/or sound modifier.
- The soft mapping of the Ge’ez characters on the standard QWERTY keyboard keys.
Future Work
We have put the following recommendations to potentially increase the efficiency of typing in the proposed Ge’ez keyboard layout.
- No quantitative studies were conducted as to the frequency of occurence and key positioning in aligning the Ge’ez first-order characters (ግእዝ) on the QWERTY keyboard keys, and future works can consider doing so to increase the efficiency of typing.
- No quantitative comparisons were conducted with regards to the performance of the proposed Ge’ez keyboard layout against the existing ones. Future works can benefit from such comparisons in articulating the performance of the proposed Ge’ez keyboard layout.
References
Positional Number System Representation Using Ge’ez Numeric Symbols
1. Introduction
This article is directed to the positional representation or place-value notation of a number system using Ge’ez numeric symbols. Ge’ez numerals consist of the arithmetic numerals (1, 2, 3, 4, 5, 6, 7, 8, 9) and the geometric numerals (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 10000) represented as (፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱) and (፲, ፳, ፴, ፵, ፶, ፷, ፸, ፹, ፺, ፻, ፼), respectively. The Ge’ez number system is a base 10 number system represented in sign-value notation, and has no representation for the number and digit zero (0). The Ge’ez number system fails to represent very small and very large numbers. For this reason, the Ge’ez number system cannot be used in scientific number system representations. However, Ge’ez numeric symbols can be made applicable to represent all the different sets of numbers (Whole numbers, Integers, Rational, Real, complex, and etc…) by using the existing Ge’ez arithmetic numerals in the standard positional number system notation, and introducing and adopting the number and digit zero (0).
2. Background
A number [1] is a mathematical object used to count, measure, and label. The different categories, called sets, of numbers are Natural numbers, Whole numbers, Integers, Rational numbers, Real numbers, and Complex numbers.
- Natural Numbers (N), also called positive integers or counting numbers, are the numbers {1, 2, 3, 4, 5, …} [2].
- Whole Numbers (W) is the set of natural numbers, plus zero, i.e., {0, 1, 2, 3, 4, 5, …} [3].
- Integer (Z) is the set of all whole numbers plus all the negatives (or opposites) of the natural numbers, i.e., {… , -2, -1, 0, 1, 2, …} [4].
- Rational Number (Q), is all the fractions where the top and bottom numbers are integers; e.g., 1/2, 3/4, 7/2, -4/3, 4/1. Note: The numerator can be 0, but not the denominator [5].
- Real Numbers (R), also called measuring numbers or measurement numbers, include all numbers that can be represented in decimal notation [6]. This includes fractions written in decimal form e.g., 0.5, 0.75 2.35, -0.073, 0.3333, or 2.142857. It also includes all the irrational numbers such as π, √2 etc. Every real number corresponds to a point on the number line.
- Complex Numbers (C) include real numbers, imaginary numbers, and sums and differences of real and imaginary numbers [7].
Generally, each number set can be expressed as a proper subset of the other (by abuse of notation), because each of these number systems is canonically isomorphic to a proper subset of the other. The resulting hierarchy, for example, allows talking, formally correctly, about real numbers that are rational numbers, and can be expressed symbolically by writing.
A number system is a system of writing for expressing numbers using digits or other symbols [8]. It is the mathematical notation for representing numbers of a given set by using digits or other symbols in a consistent manner. It provides a unique representation to every number and represents the arithmetic [9] and algebraic [10] structure of the figures. It also allows us to operate arithmetic operations like addition, subtraction, division, and exponentials. A number system representation can be positional or non-positional.
In Non-Positional number system, also known as Sign-Value Notation, each symbol represents the same value regardless of its position [11]. In sign-value notation, a corresponding number of symbols represent every natural number. If the symbol / is chosen, for example, then the number seven would be represented as ///////. Tally marks [12]represent one such system still in common use. More useful still are Sign-value notations that employ special abbreviations by introducing different symbols for repetitions of symbols, and/or for certain new values. Very commonly, these values are powers of 10; so for instance, if / stands for one, − for ten and + for 100, then the number 304 can be compactly represented as +++ //// and the number 123 as + − − /// without any need for zero. A sign-value notation, however, fails to represent all the different number categories consistently, and arithmetic operations are generally complicated.
A more elegant representation of a number system is a place-value notation [13], or the Positional Number System. A single symbol, called numerical digit, is used alone (such as "2" or "5"), or in combinations (such as "25"), to represent numbers (such as the number 25). The name "digit" comes from the fact that the ten digits (Latin digitus meaning fingers) of the hands correspond to the ten symbols of the common base 10 numeral system, i.e. the decimal digits. In a positional (sometimes-called digital) number system, a numeral is a sequence of digits, which may be of arbitrary length. Each position in the sequence has a place-value, and each digit has a value. The value of the numeral is computed by multiplying each digit in the sequence by its place-value, and summing the results. Each digit in a positional number system represents an integer. For example, in decimal (base 10) the digit "1" represents the integer one, and in the hexadecimal (base 16) system, the letter "A" represents the number ten. A positional number system has one unique digit for each integer from zero (0) up to, but not including, the radix (base) b of the number system. Thus, in the positional decimal (base 10) system, the numbers 0 to 9 can be expressed using their respective numerals "0" to "9" in the rightmost "units" position. The number 12 can be expressed with the numeral "2" in the units position, and the numeral "1" in the "tens" position, to the left of the "2", while the number 312 can be expressed by three numerals: "3" in the "hundreds" position, "1" in the "tens" position, and "2" in the "units" position.
The numerals used when expressing numerals with digits or symbols can be categorized into two - called the Arithmetic Numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) and the Geometric Numerals (1, 10, 100, 1000, 10000 ...), respectively [14]. The sign-value systems use only the geometric numerals and the positional systems use only the arithmetic numerals. A sign-value system does not need arithmetic numerals because they are made by repetition (except for the Ionic system [15]), and a positional system does not need geometric numerals because they are made by position. However, both arithmetic and geometric numerals may be used in spoken languages.
Arithmetic operations [16] (like addition, subtraction, division, exponentials, etc…) are much easier in positional systems than in the earlier additive ones (sign-value notations); furthermore, additive systems need a large number of different symbols for the different powers of 10; a positional system needs only ten different symbols (assuming that it uses base 10). Presently, the positional decimal system is universally used in human writing. The base 1000 is also used (albeit not universally), by grouping the digits and considering a sequence of three decimal digits as a single digit. This is the meaning of the common notation 1,000,234,567 used for very large numbers. In computers and other electronic devices, the main numeral systems are based on the positional system in base 2 (binary numeral system), with 2 binary digits, 0 and 1. Positional systems obtained by grouping binary digits in three (octal numeral system) or four (hexadecimal numeral system) are also commonly used. The octal (base 8) system uses the digits from "0" through "7". The hexadecimal system uses all the "0" through "9" digits from the decimal (base 10) system, plus the letters "A" through "F", which represent the numbers 10 to 15 respectively. For very large integers, bases 32 or 64 (grouping binary digits by 32 or 64, the length of the machine word) are used.
Not all languages have numeral systems. Specifically, there is not much need for numeral systems among hunter-gatherers who do not engage in commerce. Many languages around the world have no numerals [17] above two to four, or at least did not, before contact with the colonial societies. Speakers of these languages may have no tradition of using the numerals they have for counting. Indeed, several languages from the Amazon [18] have been independently reported to have no specific words for numbers other than 'one’, and some languages of Australia [19] do not have words for quantities above two. Such languages do not have a word class of 'numeral' (called Anumeric). Most languages with both numerals and counting systems use base 8, 10, 12, or 20. It is believed that base 10 number system appears to come from counting one's fingers, base 20 from the fingers and toes, base 8 from counting the spaces between the fingers, and base 12 from counting the knuckles (3 each for the four fingers). Majorities of the traditional number systems are decimal (ancient Latin adjective decem meaning ten) [20]. However, before the positional numeral system that included the number and digit zero, traditional number systems were simply used for commerce and were all represented by the sign-value notation with no zero. With the growth of civilizations and spread of education, the need to represent very large and very small numbers, have made traditional systems superseded by the use of scientific notation, or the positional system.
The first true written positional numeral system is considered to be the Hindu–Arabic numeral system [21]. This system was first used in the 7th century in India, but was not yet in its modern form because the use of the digit zero had not yet been widely accepted. Instead of a zero (0), the digits were sometimes marked with dots to indicate their significance, or a space was used as a placeholder. Even when zero (0) was introduced to the world, it was not treated as a number at that time, but as a "vacant position". Records show that the Ancient Greeks [22] seemed unsure about the status of zero (0) as a number, and asked themselves "how can 'nothing' be something?" leading to interesting philosophical and, by the Medieval period, religious arguments about the nature and existence of zero (0). They even questioned whether 1 was a number.
The first known documented use of zero (0) dates to AD 628, and appeared in the Brāhmasphuṭasiddhānta [23], the main work of the Indian mathematician Brahmagupta [24]. He treated zero (0) as a number and discussed rules governing the use of it. This work considers not only zero, but also negative numbers and the algebraic rules for the elementary operations of arithmetic with such numbers. In some instances, his rules differ from the modern standard, specifically the definition of the value of zero divided by zero as zero. Indian texts used a word śūnya (Sanskrit: शून्य) [25] to refer to the concept of void. In AD 813, a Persian mathematician, Muḥammad ibn Mūsā al-Khwārizmī [26], prepared astronomical tables using Hindu numerals; and about AD 825, he published a book synthesizing Greek and Hindu knowledge of astronomy and contained his own contribution to mathematics including an explanation of the use of zero. This book was later translated into Latin in the 12th century under the title Algoritmi de numero Indorum [27]. This title means "al-Khwarizmi on the Numerals of the Indians". The word "Algoritmi" was the translator's Latinization of Al-Khwarizmi's name, and the word "Algorithm" or "Algorism" started meaning any arithmetic based on decimals [28]. Muhammad ibn Mūsā al-Khwarizmi stated that if no number appears in the place of tens in a calculation, a little circle should be used to "keep the rows". This circle was called ṣifr. In pre-Islamic time, the word ṣifr (Arabic صفر) had the meaning "empty" [29]. The Hindu–Arabic numeral system (base 10) [21] reached Europe in the 11th century via Al-Andalus through Spanish Muslims, the Moors, together with knowledge of astronomy and instruments like the astrolabe [30]. For this reason, the Hindu–Arabic numeral system [21] came to be known in Europe as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa (1170–1250), who grew up in North Africa, was instrumental in bringing the system into European mathematics in 1202 [31]. He used the term zephyrum for the Arabic ṣifr. This became zefiro in Italian, and was then contracted to zero in Venetian. The Italian word zefiro was already in existence (meaning "west-wind" from Latin and Greek zephyrus) and may have influenced the spelling when transcribing the Arabic ṣifr. Sifr evolved to mean zero when it was used to translate śūnya from India. By the 13th century, Western Arabic numerals were accepted in European mathematical circles. They began to enter common use in the 15th century. Until the late 15th century, Hindu–Arabic numerals seem to have predominated among mathematicians, while merchants preferred to use the Roman numerals. In the 16th century, they became commonly used in Europe. The first known English use of zero was in 1598. By the end of the 20th century, virtually all non-computerized calculations in the world were done with Arabic numerals, which have replaced native numeral systems in most cultures.
Zero (0) is both a number and the numeric digit used to represent that number in positional number systems. As a digit, it is used as a placeholder in place-value systems. Below are some of its scientific applications.
-
The number zero (0) fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures [22]. Zero is the integer immediately preceding 1. Zero is an even number, because it is divisible by 2 with no remainder. Zero (0) is neither positive nor negative. Many definitions include Zero (0) as a natural number, and then the only natural number not to be positive. Zero (0) is a number which quantifies a count or an amount of null size. In most cultures, Zero (0) was identified before the idea of negative things, or quantities less than zero, was accepted. The value, or number, Zero (0) is not the same as the digit zero, used in numeral systems using positional notation. Successive positions of digits have higher weights, so inside a numeral the digit zero is used to skip a position and give appropriate weights to the preceding and following digits. A Zero (0) digit is not always necessary in a positional number system, for example, in the number 02. In some instances, a leading Zero (0) may be used to distinguish a number. The number Zero (0) is the smallest non-negative integer. The natural number following Zero (0) is 1 and no natural number precedes Zero (0). The number Zero (0) may or may not be considered a natural number, but it is an integer, and hence a rational number and a real number (as well as an algebraic number and a complex number). The number Zero (0) is neither positive nor negative and is usually displayed as the central number in a number line. It is neither a prime number nor a composite number. It cannot be a prime because it has an infinite number of factors, and cannot be composite because it cannot be expressed as a product of prime numbers (0 must always be one of the factors). Zero (0) is, however, even (as well as being a multiple of any other integer, rational, or real number).
The following are some basic (elementary) rules for dealing with the number 0 [22]. These rules apply for any real or complex number x, unless otherwise stated.
- Addition: x + 0 = 0 + x = x. That is, 0 is an identity element (or neutral element) with respect to addition.
- Subtraction: x − 0 = x and 0 − x = −x.
- Multiplication: x • 0 = 0 • x = 0.
- Division: 0/x = 0, for non-zero x. But x/0 is undefined, because 0 has no multiplicative inverse (no real number multiplied by 0 produces 1), a consequence of the previous rule.
- Exponentiation: x0 = x/x = 1, except that the case x = 0 may be left undefined in some contexts. For all positive real x, 0x = 0.
The sum of 0 numbers (the empty sum) is 0, and the product of 0 numbers (the empty product) is 1. The factorial of Zero (0!) is evaluated to 1, as a special case of the empty product.
In set theory [22], 0 is the cardinality of the empty set: if one does not have any apples, then one has 0 apples. In fact, in certain axiomatic developments of mathematics from set theory, 0 is defined to be the empty set. When this is done, the empty set is the von Neumann cardinal assignment [32] for a set with no elements, which is the empty set. The cardinality function, applied to the empty set, returns the empty set as a value, thereby assigning it 0 elements. Also in set theory, 0 is the lowest ordinal number, corresponding to the empty set viewed as a well-ordered set. In propositional logic [33], 0 may be used to denote the truth value false. In abstract algebra [34], 0 is commonly used to denote a zero element, which is a neutral element for addition (if defined on the structure under consideration) and an absorbing element for multiplication (if defined). In lattice theory [35], 0 may denote the bottom element of a bounded lattice. In category theory [36], 0 is sometimes used to denote an initial object of a category. In recursion theory [37], 0 can be used to denote the Turing degree of the partial computable functions.
A zero of a function [22] f is a point x in the domain of the function such that f(x) = 0. When there are finitely many zeros these are called the roots of the function. This is related to zeros of a holomorphic function. The zero function (or zero map) on a domain D is the constant function with 0 as its only possible output value, i.e., the function f defined by f(x) = 0 for all x in D. The zero function is the only function that is both even and odd. A particular zero function is a zero morphism in category theory; e.g., a zero map is the identity in the additive group of functions. The determinant on non-invertible square matrices is a zero map. Several branches of mathematics have zero elements, which generalize either the property 0 + x = x, or the property 0 • x = 0, or both.
-
The value zero plays a special role for many physical quantities [38]. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, for an absolute temperature [39] (as measured in Kelvin) zero is the lowest possible value (negative temperatures are defined, but negative-temperature systems are not actually colder). This is in contrast to—for example, temperatures on the Celsius scale, where zero is arbitrarily defined to be at the freezing point of water. Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value—for example, at a value for the threshold of hearing. In physics, the zero-point energy [40] is the lowest possible energy that a quantum mechanical physical system may possess and is the energy of the ground state of the system.
-
Zero has been proposed as the atomic number of the theoretical element tetra-neutron [41]. It has been shown that a cluster of four neutrons may be stable enough to be considered an atom in its own right. This would create an element with no protons and no charge on its nucleus. As early as 1926, Andreas von Antropoff [42] coined the term neutronium for a conjectured form of matter made up of neutrons with no protons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table [43]. It was subsequently placed as a noble gas in the middle of several spiral representations of the periodic system for classifying the chemical elements.
-
The most common practice throughout human history has been to start counting at one, and this is the practice in the early classic computer science programming languages such as FORTRAN [44] and COBOL [45]. However, in the late 1950s, LISP introduced zero-based numbering for arrays while ALGOL, introduced completely flexible basing for array subscripts (allowing any positive, negative, or zero integer as base for array subscripts) [46], and most subsequent programming languages adopted one or other of these positions. For example, the elements of an array are numbered starting from 0 in C [47], so that for an array of n items the sequence of array indices run from 0 to n−1. This permits an array element's location to be calculated by adding the index directly to address of the array, whereas 1-based languages pre-calculate the array's base address to be the position one element before the first. There can be confusion between 0- and 1-based indexing, for example Java's JDBC [48] indexes parameters from 1 although Java itself uses 0-based indexing. In databases, it is possible for a field not to have a value. It is then said to have a null value. For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result. A null pointer is a pointer in a computer program that does not point to any object or function. In C [47], the integer constant 0 is converted into the null pointer at compile time when it appears in a pointer context, and so 0 is a standard way to refer to the null pointer in code. However, the internal representation of the null pointer may be any bit pattern (possibly different values for different data types). In mathematics −0 = +0 = 0; both −0 and +0 represent exactly the same number, i.e., there is no "positive zero" or "negative zero" distinct from zero. However, in some computer hardware signed number representations, zero has two distinct representations, a positive one grouped with the positive numbers and a negative one grouped with the negatives; this kind of dual representation is known as signed zero, with the latter form sometimes called negative zero. These representations include the signed magnitude and one's complement binary integer representations (but not the two's complement binary form used in most modern computers), and most floating point number representations (such as IEEE 754 [49] and IBM S/390 [50] floating point formats). In binary, 0 represents the value for "off", which means no electricity flow. Zero is the value of false in many programming languages. Many APIs and operating systems that require applications to return an integer value as an exit status [51] typically use zero to indicate success and non-zero values to indicate specific error or warning conditions.
Ge’ez [52], which is one of the world's most ancient alphabets and languages, is used in Ethiopia and Eritrea to writing Ge’ez, Tigrigna, Amharic, etc..., languages. It has its own scripting characters, which consist of letters, punctuations and numeric characters. Ge’ez numeric symbols consist of the arithmetic numerals (1, 2, 3, 4, 5, 6, 7, 8, 9) and the geometric numerals (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 10000), represented as (፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱) and (፲, ፳, ፴, ፵, ፶, ፷, ፸, ፹, ፺, ፻, ፼), respectively. The ancient civilization, which might date back to Axum [53], only needed a number system for the counting numbers, or a method of counting, and used a base 10 (or decimal) number system, believed to have come from counting with one's fingers, represented by a sign-value notation. Although the concept of "nothing" or "empty" was obvious to the religious people of this civilization, the number and digit zero has no representation in Ge’ez numeric symbols. Representation of counting numbers in Ge’ez is additive using its arithmetic and geometric numerals. However, it gets inconsistent for very large numbers and cannot have all the representations for them. The Ge’ez number system, base 10 sign-value notation with no zero, cannot represent all the different number types and consistently, and even the simplest arithmetic operations are generally complex in sign-value notation. Moreover, there are no Ge’ez representations for decimal numbers. Therefore, the Ge’ez number system cannot represent very large and very small numbers. For this and other reasons, we cannot use Ge’ez numerals in scientific applications, such as business, education and technology. We witnessed the "Millennium Bug" [54] that hit the world, and waited until it was our Millennium 7 years, 8 months, and 11 days later only to realize that we are unable to correctly represent it using the Ge’ez numerals, to even celebrate it! To make the matter even more complicated, we just represented it with a Ge’ez numeral and a Ge’ez word, ፪ሺህ, and posted it in bold for the public to learn from it!!!
Positional number system is believed to have come to Ethiopia not with the advancement of commerce but with the spread of modern education [55], which accounts mainly to the time of Emperor Haile Selassie-I [56]. Zero, the symbol for both the digit and the number, was also introduced along with the positional number system. The modern Ethiopia constitutionally grants its citizens the right to learn in their native languages and transcript using their native symbols (Article 39, section 2 [57]). However, the country uses the standard base 10 positional number system, or the Hindu-Arabic number system, along with the 0 through 9 Arabic numerals. In other words, Arabization [58] of the existing 1-through-9 Ge’ez numeric symbols (፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱) on an attempt to standardize the national number system. The Hindu-Arabic number system, along with its numeric symbols, is now the official national number system used in education, business and government communications in the country. This is against the constitution, and has negative social, cultural, educational and economic impacts.
3. Proposed Solution
Ge’ez numeric symbols can be made applicable to represent all the different categories of numbers by adopting the standard positional (place-value) notation and introducing the number and digit zero (0) to the already existing "1" through "9" Ge’ez arithmetic numeric symbols (፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱). This way, we can salvage the Ge’ez arithmetic numeric symbols rather than forgoing them all to the standard positional notation along with the "1" through "9" Hindu-Arabic numeric symbols, preserving our cultural values and ripping the constitutional, social, economic and all the treasures it brings along.
In a standard base-10 positional number system, the arithmetic Ge’ez numeric symbols will contain 10 symbols, i.e.,{0, ፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱}, and can be used in any scientific mathematical operations.
4. Conclusion and Future Work
Conclusion
The Positional Numbers System has become the standard number system used internationally in academics, business and government communications. However, it is a system for representing all the different concepts of numbers; it can be used with one's own traditional numeric symbols.
Ge’ez numeric symbols can be made applicable to represent the different concepts of numbers by adopting the standard positional (place-value) notation and introducing the number and digit zero (0) to the already existing "1" through "9" Ge’ez arithmetic numeric symbols (፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱).
Contribution
The main contributions of the study are listed below.
- Application of Positional Numbers System using Ge’ez numeric symbols.
- Numeric information extraction in Ge’ez descended digital texts.
- Preserving cultural values, and this in return adds social, economic and etc values.
- Help exercise, and thus strengthen, our constitutional rights.
Future Work
This study not only introduces the number and digit zero (0) but it also adopts it to the already existing Ge’ez arithmetic numeric symbols. Future works can benefit from having a Ge’ez zero (0) symbol that adheres to the nature of the existing Ge’ez arithmetic numeric symbols.
